Smokers are less likely to die of age related sickness
In this article, we will revisit the example from our Supervised Learning introduction where we needed to identify different fruits in a basket. Imagine being in an orchard, where you gather information about the fruits available. The information is presented in a table with the following attributes for each fruit:
- Name of the fruit
- Whether it is yellow or not
- Whether it is long or not
- Whether it is sweet or not
Here is a sample table showing the details about the fruits in the orchard:
| Fruit | Yellow | Long | Sweet |
|---|---|---|---|
| Mango | true | false | true |
| Apple | false | false | false |
| Mango | false | false | true |
| Banana | true | true | false |
| ... | |||
| Total | 1000 rows |
Now, given a fruit from the basket, your task is to determine if it is a mango, banana, or something else.
The core concept behind the Naive Bayes Classifier is that the attributes are considered to be conditionally independent. Even though it may not seem very practical, but being a simple algorithm this assumption is very effective.
To identify a fruit from the basket, let's say you pick up a fruit and observe that it is yellow, long, and not sweet. How can you utilize the provided table to determine the type of fruit? One way is to compute the probability of the fruit being a yellow, long and not sweet X (mango/banana/others) using Bayes’ Theorem as:
P(X, Y, L, S’) = P(Y, L, S’, X) = P(Y|L, S’, X) * P(L|S’, X) * P(S’|X) * P(X)
Here, P(Y|L, S’, X) means probability of color being yellow given that the fruit is long, not sweet and is X. P(L|S’, X), P(S’|X) have similar meanings.
In the Naive Bayes Classifier, we assume that all attributes are conditionally independent, allowing us to simplify the equation as:
P(X, Y, L, S’) = P(Y|X) * P(L|X) * P(S’|X) * P(X)
Here,
P(X): Probability of the fruit being XP(Y|X): Probability of the color being yellow given the fruit is XP(L|X): Probability of the length being long given the fruit is XP(S'|X): Probability of the sweetness type being (not sweet) given the fruit is X
The difference between both the equations is that we are assuming that P(Y|L, S’, X) = P(Y|X) since all attributes are independent. We are doing the same for other components in the equation.
Based on the details provided, we can create an aggregated table that counts the occurrences of each attribute for mangoes, bananas, and other fruits:
| Fruit | Yellow | Long | Sweet | Total Pieces |
|---|---|---|---|---|
| Mango | 200 | 0 | 250 | 300 |
| Banana | 350 | 350 | 200 | 400 |
| Others | 150 | 100 | 150 | 300 |
| Total | 700 | 450 | 600 | 1000 |
In this table, the value at (Mango, Yellow) represents the number of yellow mangoes, and the value at (Mango, Total Pieces) represents the total number of mangoes. We can similarly interpret the other cells.
From this table, we can create a likelihood table, which represents the likelihood of an event occurring:
| Fruit | Yellow | Long | Sweet | Total Pieces |
|---|---|---|---|---|
| Mango | 200/300 | 0/300 | 250/300 | 300/1000 |
| Banana | 350/400 | 350/400 | 200/400 | 400/1000 |
| Others | 150/300 | 100/300 | 150/300 | 300/1000 |
| Total | 700/1000 | 450/1000 | 600/1000 | 1000/1000 |
In this likelihood table, the value at (Mango, Yellow) represents the probability of the color being yellow given that the fruit is a mango (P(Y|M)), and the value at (Mango, Total Pieces) represents the probability of the fruit being a mango (P(M)). The other cells have similar interpretations.
Now, we have all the required probabilities to compute P(X, Y, L, S').
For example, let's calculate the probability of the fruit being a mango, given that it is yellow, long, and not sweet:
P(M, Y, L, S’) = 200/300 * 0/300 * 250/300 * 300/1000 = 0
Similarly, we can calculate the probabilities for a banana and others:
P(B, Y, L, S’) = 350/400 * 350/400 * 200/400 * 400/1000 = 0.153125
P(O, Y, L, S’) = 150/300 * 100/300 * 150/300 * 300/1000 = 0.025
Therefore, the individual probabilities of the fruit being a mango, banana, or others, given that it is yellow, long, and not sweet, are:
P(M | Y, L, S’) = 0/(0+0.153125+0.025) = 0
P(B | Y, L, S’) = 0.153125/(0+0.153125+0.025) = 0.86
P(O | Y, L, S’) = 0.025/(0+0.153125+0.025) = 0.14
Since the probability of it being a banana is the highest, we can conclude that the fruit is a banana. This approach can be applied to all the fruits in the basket, resulting in accurate identification with high precision.
One drawback of using the Naive Bayes Classifier is the assumption of attribute independence, which may not always hold true.
The Naive Bayes classifier is available in scikit-learn as GaussianNB, MultinomialNB, and BernoulliNB in the sklearn.naive_bayes module.
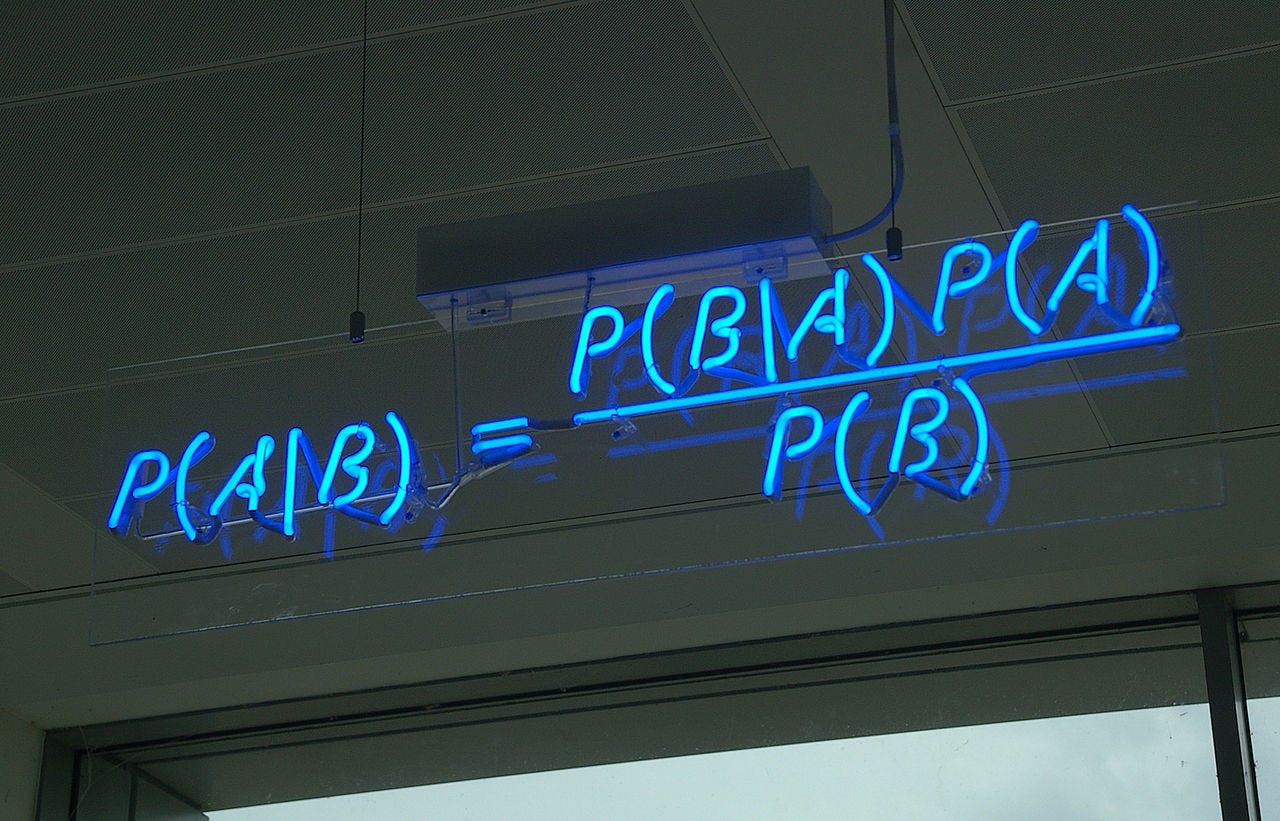 Image Source: wikipedia
Image Source: wikipedia