Binary Classification

2023-07-09

To be, or not to be: that is the question

Introduction

Binary Classification is the task of classifying elements into one of two classes/groups. Some examples include determining if a person has a particular disease, classifying email as spam or not spam, and detecting credit card fraud. It is a form of supervised learning where a model is trained based on a set of observations, and then used to classify new observations into categories.

Methods

Some commonly used methods for binary classification are:

The choice of method depends on the problem and available data. According to the No Free Lunch Theorem, any two optimization algorithms are equivalent when their performance is averaged across all possible problems. It is recommended to start with simpler methods and consider more complex ones if needed.

Evaluation

The most common evaluation metric for binary classification is accuracy. It is defined as:

Accuracy = (# Correct Predictions)/(# Observations)

However, accuracy may not always be the best metric for every use case. For example, in the case of cancer detection, if most samples are negative (no cancer), a model that predicts all samples as negative would still achieve high accuracy. However, this is undesirable because we don't want to mistakenly tell a person with cancer that they don't have the disease. Instead, we can request further tests for individuals without cancer, if necessary. Therefore, we would want a model that minimizes the prediction of positive cases as negative, i.e., has a higher recall.

Let's consider a scenario where our observations consist of both positive (P) and negative (N) samples. The model provides two types of predictions: predicted positive (P') and predicted negative (N'). By analyzing these predictions, we can construct a confusion matrix as shown below:

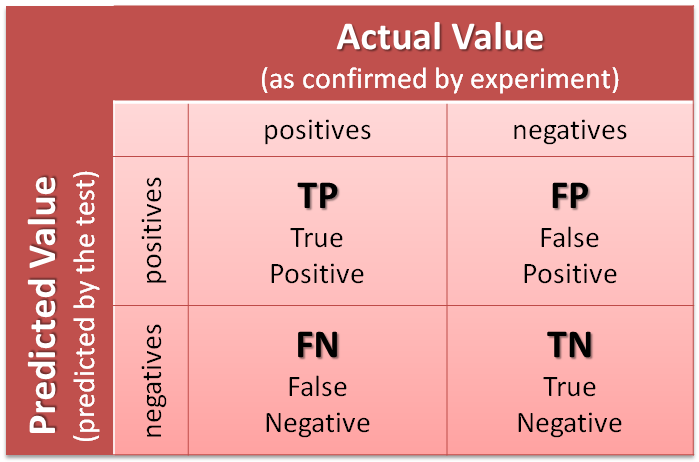Confusion Matrix (Source: MathWorks)

In the confusion matrix, we have the following categories:

From the confusion matrix, we can observe the following relationships:

  • P + N = Total number of observations.
  • TP + TN = Number of true (correct) predictions.
  • FP + FN = Number of false (incorrect) predictions.
  • TP + FN = Total number of positive samples (P).
  • TN + FP = Total number of negative samples (N).
  • TP + FP = Total number of predicted positive samples (P').
  • TN + FN = Total number of predicted negative samples (N').

Therefore, Accuracy (ACC) = (TP + TN)/(P + N)

We can derive 8 more useful metrics based on TP, FP, TN, FN. These are:

Further Derivations:

Sample Values:

Actual Predicted
1 1
0 0
0 1
1 0
1 1
0 0
0 0
1 0

Metrics:

P = 4
N = 4
P' = 3
N' = 5

TP = 2
TN = 3
FP = 1
FN = 2

P + N = 8
TP + TN = 5
FP + FN = 3
TP + FN = P = 4
TN + FP = N = 4
TP + FP = P' = 3
TN + FN = N' = 5
ACC = (TP + TN)/(P + N) = 5/8 = 0.625

Recall/TPR = TP/P = 2/4 = 0.5
FNR = FN/P = 2/4 = 0.5
TNR = TN/N = 3/4 = 0.75
FPR = FP/N = 1/4 = 0.25
Precision/PPV = TP/P' = 2/3 = 0.67
FDR = FP/P' = 1/3 = 0.33
NPV = TN/N' = 3/5 = 0.6
FOR = FN/N' = 2/5 = 0.4

LR+ = TPR/FPR = 0.5/0.25 = 2
LR- = FNR/TNR = 0.5/0.75 = 0.67

Another commonly used evaluation metric is AUC (Area under the curve)/ROC (Receiver operating characteristic) curve score.

ROC Curve

ROC Curve (Source:Wikipedia)

A ROC space is defined by FPR and TPR as x and y axes, respectively, which depicts relative trade-offs between true positive (benefits) and false positive (costs). The ROC curve is created by plotting the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings. AUC is the area under the ROC Curve. A higher AUC score signifies a better model.